How Robots Walk 2025-04-25
This is a tour of the code for a walking robot. Everything is open-source, so you can download, run, and modify the walking code and the visualization system. The interesting code, which does all the balance and control feedback, is only about 300 lines. The walking isn't awesome – it's slow and not very steady – but it demonstrates many of the hard control problems involved in robot walking.
Here's what the simulated robot does.
The walking code has to do the following:
- Generate a repeating pattern, the left-right-left-right of walking
- Estimate the robot's orientation relative to gravity, it's velocity relative to the ground, and the position of the feet in the inertial coordinate system. This is easier (but still not trivial) on a simulator than on hardware.
- Generate baseline angles and torques for the joints
- Generate baseline inertial positions of the feet while walking, and compare to the actual positions
- When the robot is slightly out of position, apply feedback to correct it. There are several more ways to be out of position than falling front-back or left-right that need to be actively corrected.
- When the simulation starts, achieve a stable standing position before starting to walk.
- Start and stop walking at the right point in the cycle.
The robot here is a simulation of a humanoid, part of Mujoco's standard library. Without the code presented below, it just faceplants.
The graphics here are captured from the throbol editor. Throbol is a programming language for robots, and the editor is a kind of spreadsheet for real-time control problems. It has cells and formulas like a conventional spreadsheet, but a cell's value is a time series instead of just a single value. Below each formula it shows a graph of the value over the duration of the simulation, which here is 10 seconds.
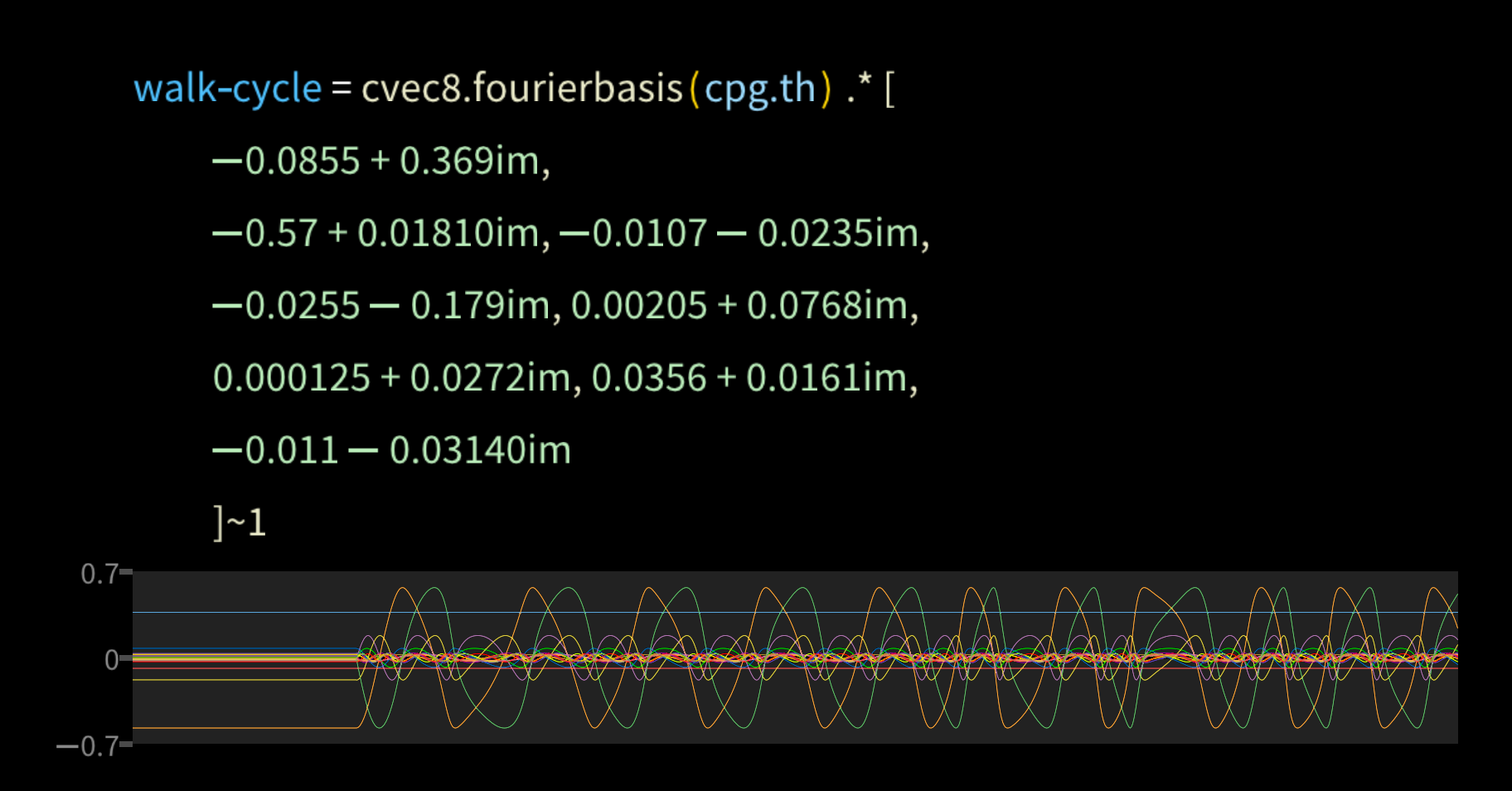
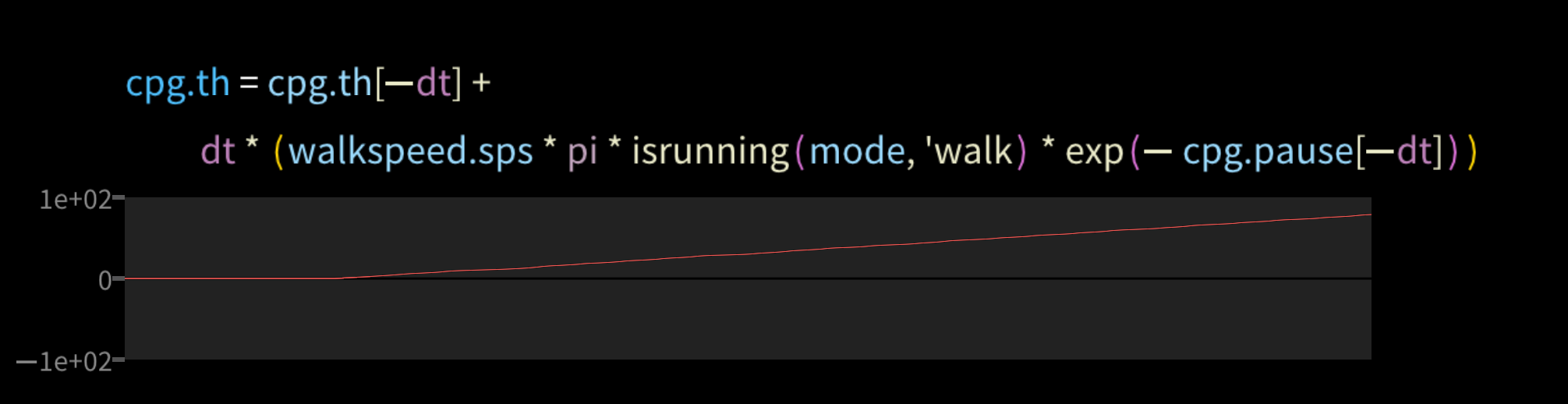
Let's start with the central pattern generator. Walking is a cycle, and cyclic patterns can be represented as a Fourier series. So we take the dot product of a 8-term Fourier basis and some experimentally derived coefficients.
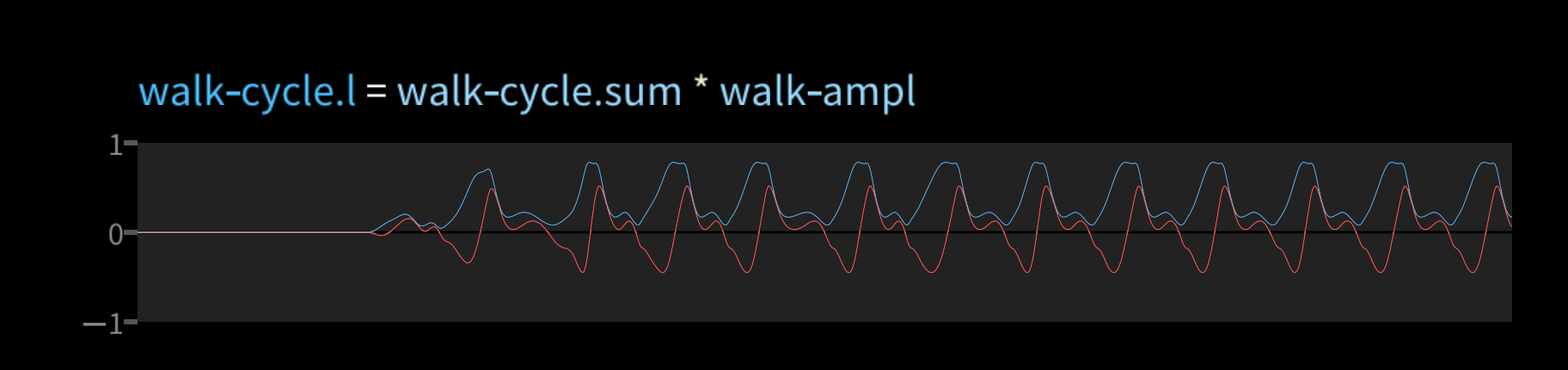
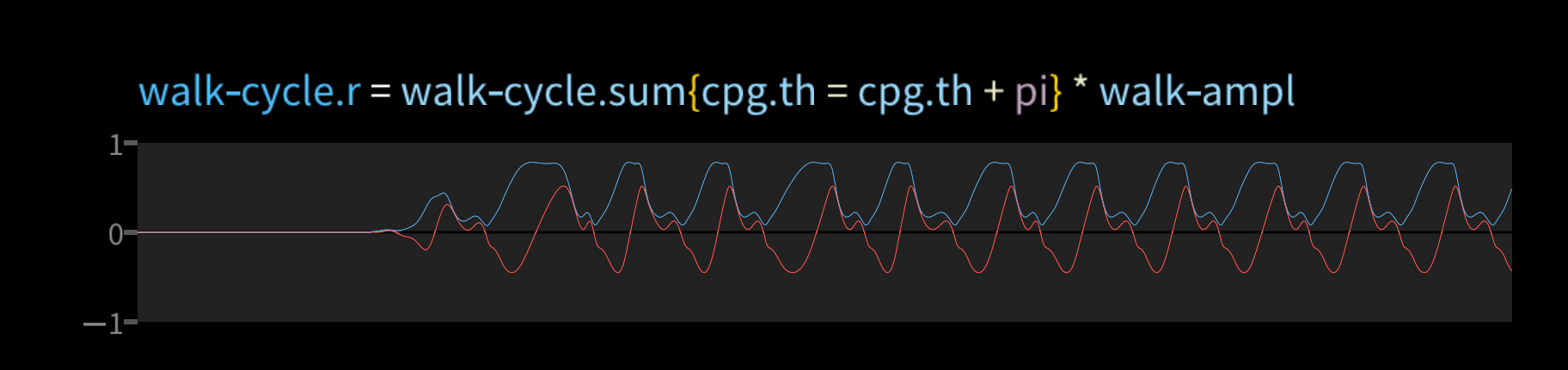
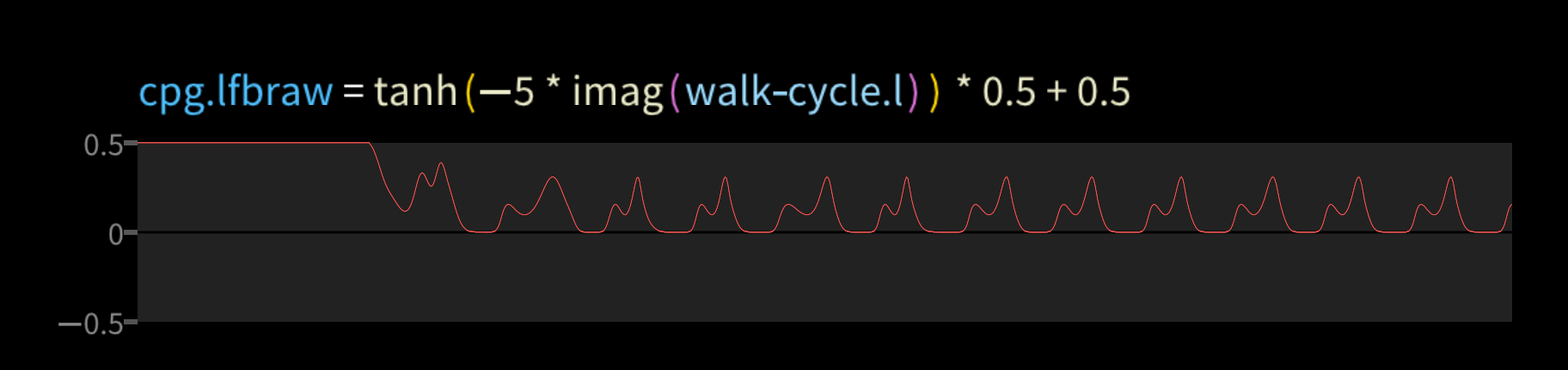
We then make a left and a right side of the cycle, offset by pi radians. These are complex numbers, so the graphs show the real part in red and the imaginary part in blue.
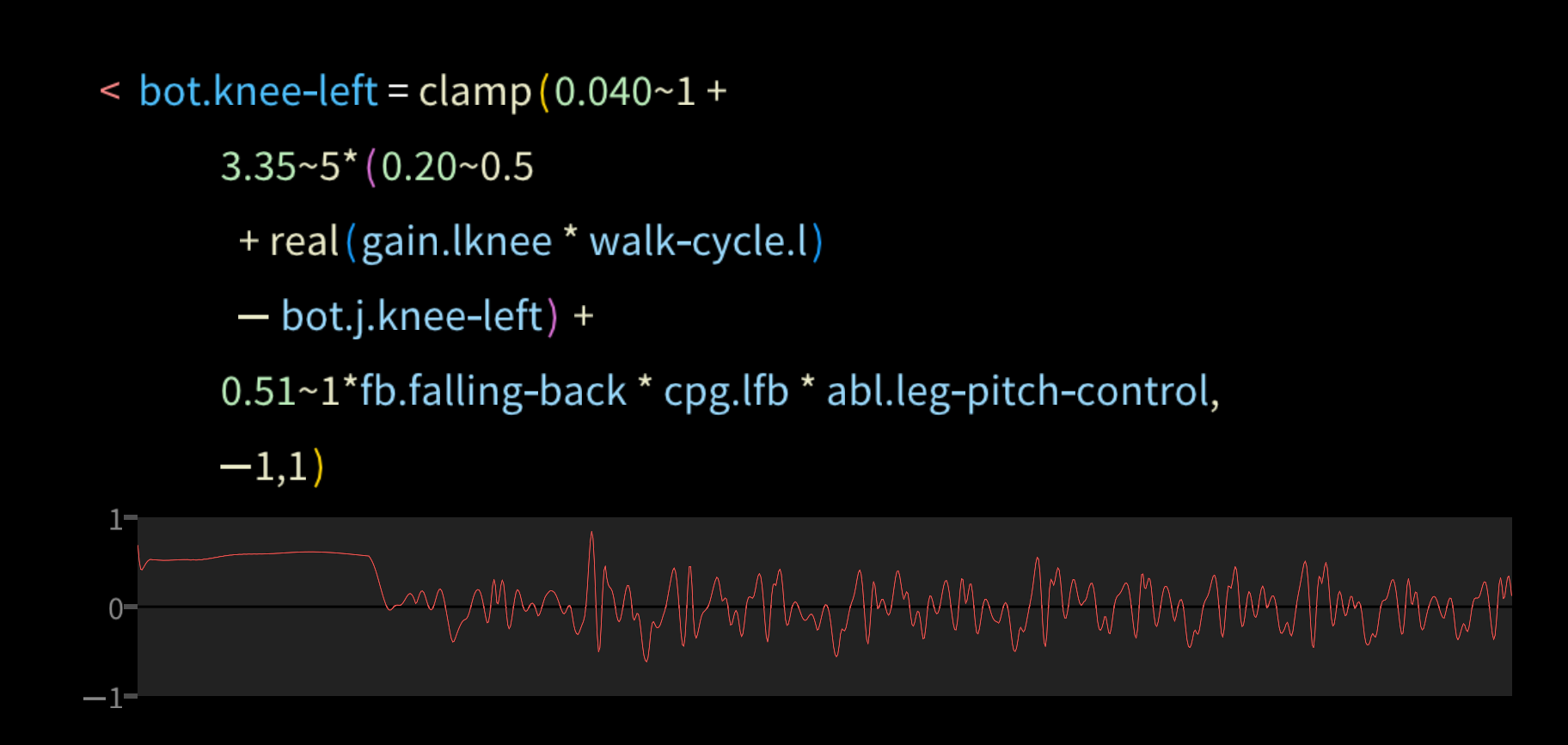
We can then drive the leg motion from these cyclic values. Here's the left knee joint, for example.
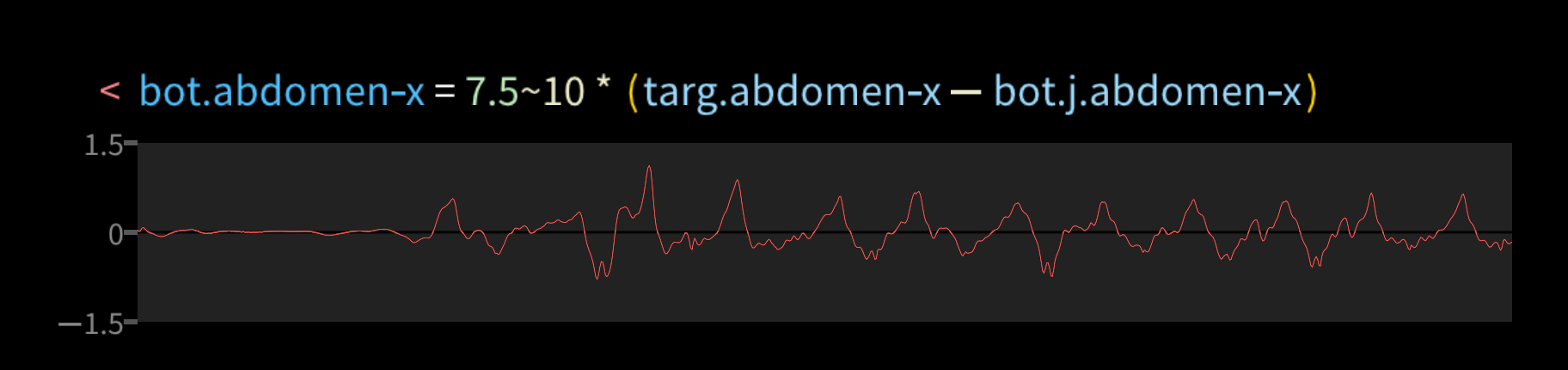
There's a lot going on in that formula, so let's look at a simpler one and build up from there. This formula below controls the abdomen X axis joint, which makes it bend left or right at the waist. It's a simple "P" control loop, where the joint torque (bot.abdomen_x) is a constant (7.5) times the difference between the target position (targ.abdomen_x) and the measured position (bot.j.abdomen_x).
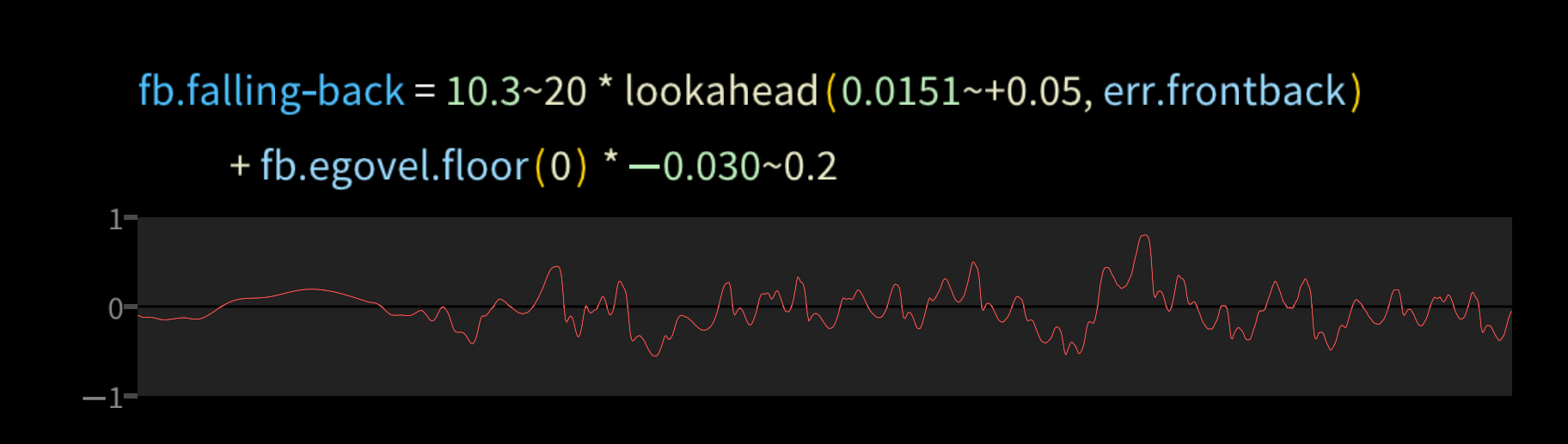
The knee joint formula above includes some more terms in the feedback loop, including feedback from a balance error cell fb.falling_back. Its value is positive when the robot is falling back, negative when falling forward.
The lookahead function predicts the time series ahead by a short interval, by adding in the velocity measured between the previous and current timesteps. It's calculated like this.
lookahead(duration, x) = x + (duration/dt) * (x - x[-dt])
where dt is the timestep of the control code.
The other term in the feedback is egovel.floor: the velocity of the floor relative to the egocenter of the robot. In robotics, it's usually best to work with egocentric coordinates, where some point in the robot's body is defined as [0,0,0] and the world moves around it. It's an inertial coordinate system, meaning that Z is up relative to gravity rather than pitching and rolling with the robot. However it does track the robot's yaw. egovel.floor is a 3-vector, and for the front-back balance we extract only the X coordinate.
But let's look at the major term in the feedback, err.frontback. It's a little gnarlier:
The key idea here is that where the feet are matters more at some points in the walk cycle than others. We need to apply strong feedback if the feet on the ground are slightly away from where we expected them, but not when they're in the air. This is driven by cpg.lfb and cpg.rfb, which say how important left and right foot errors are at any point. As the name suggests, they come from the central pattern generator.
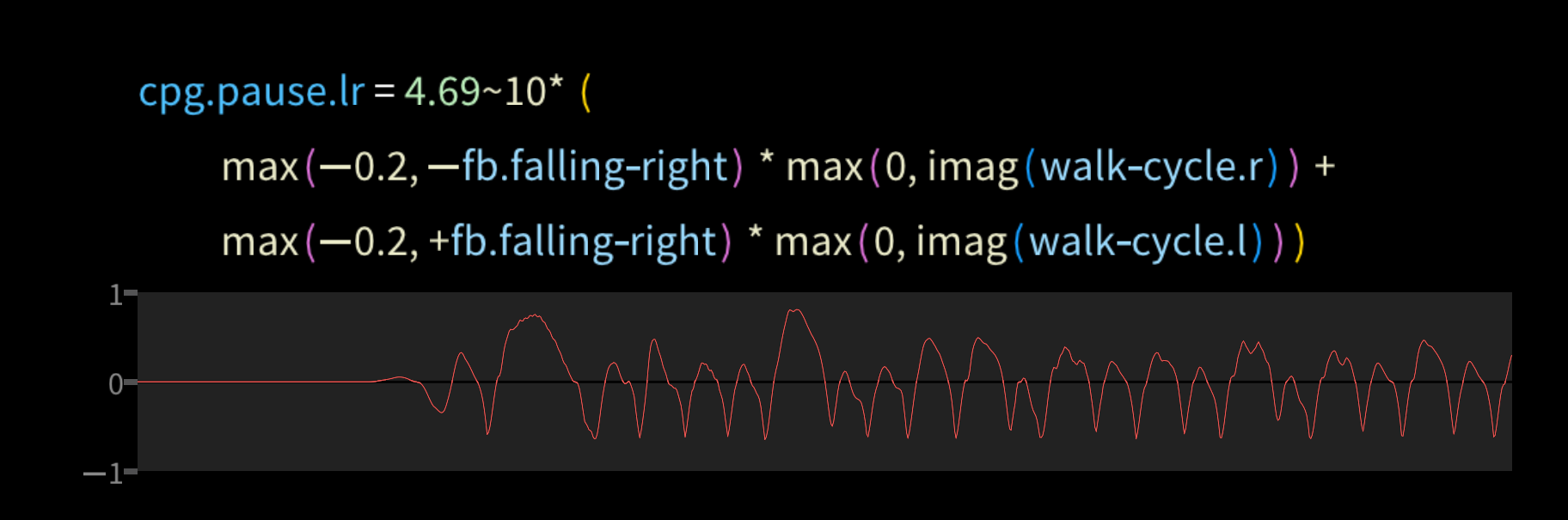
You may notice how irregular the timing is. That's because the CPG is itself affected by feedback, as it must be for balance. To visualize why, imagine the robot is on its right foot and also teetering over to the right. It needs to take a little longer before switching to the left foot. So the CPG's phase increases at a rate depending on cpg.pause.
For example, it pauses if it's falling right and it's on the right half of the cycle, and vice-versa.
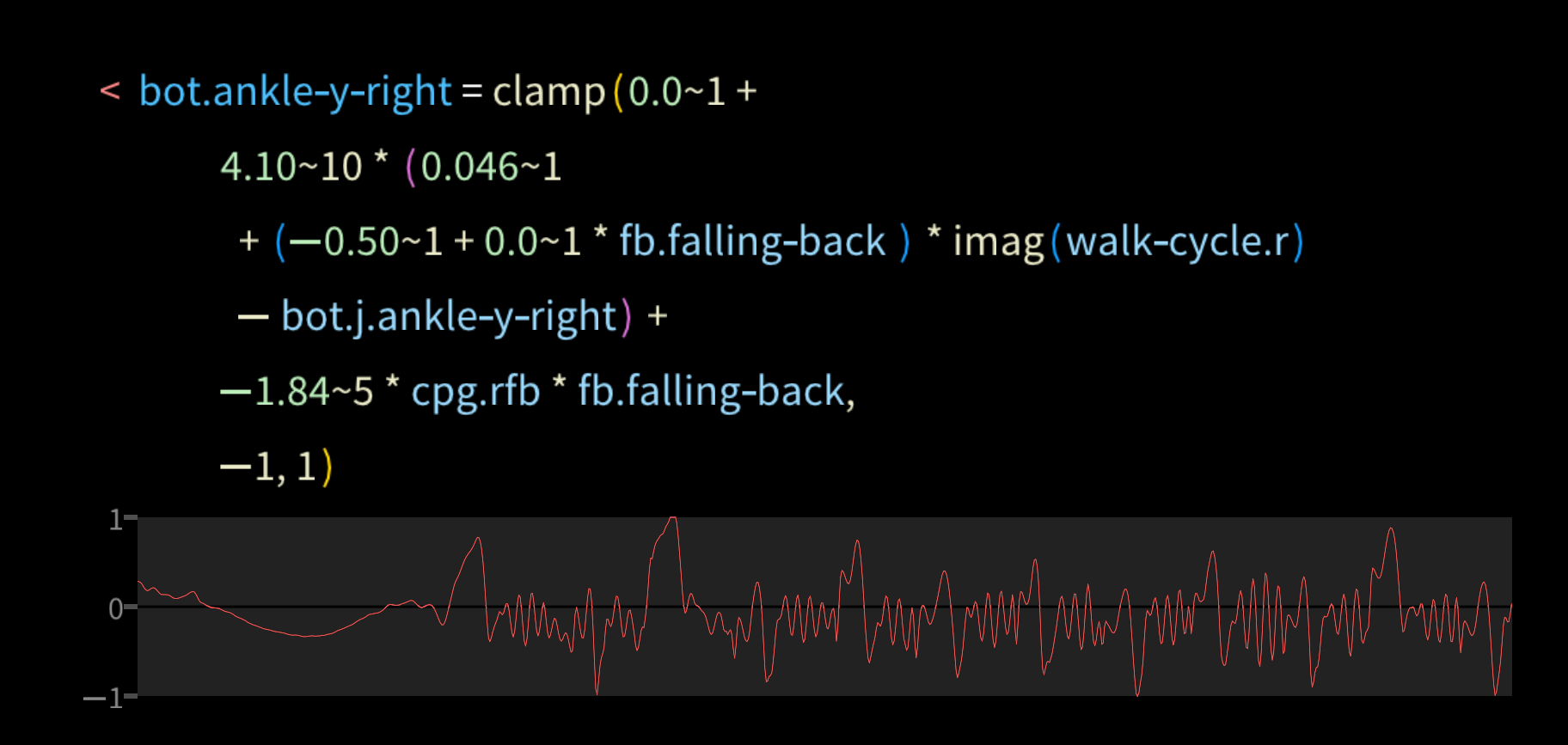
We also use these feedback terms to gate applying torque at the ankles to stabilize the robot. This has to be done whether or not it's walking.
You may have wondered by many numbers are written like the 4.10~10 above. The ~ syntax in throbol marks an adjustable parameter, here with a range of [-10 .. 10]. There's no theoretical reason for this feedback coefficient to be 4.1, it's just a number that seems to work. 4.0 would work about the same. 3.0 would probably work, but the robot would be a bit more wobbly. 1.0 may not be enough to keep is upright. 10.0 might cause violent feedback oscillation in the ankles. In robotics, most numbers are like this, so the language is designed to make it easy to adjust them. In the throbol editor, you can hover over a number market with ~range and shift-drag the mouse to change it and see the simulation results change interactively. It also works on live hardware within the limits of causality. Meaning: in simulation mode it redoes the whole simulation from the beginning when you change a parameter, but in live hardware mode it only changes it for the rest of the run.
There are also some numerical optimization tools to automatically tune parameters, if you write a fitness function. See the article Optimization in Throbol for more about this.
One of the key tools in working with feedback loops is comparing the results with slightly different perturbations. You want the robot to follow the trajectory despite some noise in the actuators, irregular ground, wind, etc. So it's useful to look at the dispersion across a range of disturbances. There are several tools for analyzing this, but the most intuitive is a video that superimposes 10 instances of the robot.
The best way to build intuition for robot walking is to experiment. Change parameters and see how things get worse or better. All this stuff is open-source. The easy way to start is to download throbol and run it. It has humanoid_walking.tb as one of the example projects. Or if you enjoy building big C++ projects with Rust dependencies, you can build it from source for Mac or Linux.
Here's my wish list for how the walking should be better:
- It swings its arms side-to-side a lot which looks dorky.
- There's some oscillation in the joint feedback loops. You can see it in the bot.ankle_y_right graph above.
- It takes small steps. It should walk faster.
- The walking speed feedback is weak. If it's under-speed, it needs to lean forward more.
- The direction control code is primitive. It should be able to follow a heading.